Plotting with Maple
Copyright Michael Sullivan, 2006
Basic plotting.
Maple has a powerful set of graphing tools. The two
with
commands below load in the graphing commands we need. The
restart
clears the memory. We shall start each section with these three commands. SOme basic plotting commands are loaded by default. Change the colons to semi-colons and notice wht happens.
Warning, the name changecoords has been redefined
Warning, the assigned name arrow now has a global binding
We can define a function f(x) as follows:


To get the result in floating point format we use the
evalf
command:
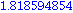
Now we do a simple plot of f(x).
| > |
plot(f(x),x=-3*Pi..3*Pi,y=-5..10, color=black,thickness=2); |
![[Plot]](images/plotting_4.gif)
Next we do a rational function.
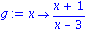
| > |
plot(g(x),x=-5..5,y=-10..10,color=black,thickness=2); |
![[Plot]](images/plotting_6.gif)
Maple does not understand vertical asymptotes. But it will know what do do if we give it hint! The option "discont=true" tells Maple that the function may have discontinuities. Then Maple will skip other them.
| > |
plot(g(x),x=-5..5,y=-10..10,color=black,thickness=2,discont=true); |
![[Plot]](images/plotting_7.gif)
Graphs can be overlayed.
| > |
plot([f(x),g(x)],x=-10..10,y=-10..10,discont=true,color=[red,blue],thickness=2); |
![[Plot]](images/plotting_8.gif)
Here and below you can use the HELP button (top right-hand corner) to look up information about any command or option. You should practice a few graphs of your own before going on.
Example 1: Marking special points.
| > |
restart;with(plots):with(plottools): |
Warning, the name changecoords has been redefined
Warning, the assigned name arrow now has a global binding
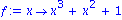
We find the extrema. We use the
diff
command and then the
solve
command.

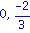
These are the critical numbers. We evaluate the function f(x) at these two numbers.
Next we find the second derivative.
Clearly f(0) is a relative min and f(-2/3) is a relative max. We also see that the inflection point is at x=-1/3.
Note: Obviously you do not need computer to analyze a cubic. We are starting with easy examples to learn how Maple works. Using a computer or calculator to solve such an easy problem will, in general, hurt your learning.
Now we are ready to set up our graph.
| > |
Min:=disk([0,1], 0.03, color=red): |
| > |
Max:=disk([-2/3,31/27], 0.03, color=red): |
| > |
Inflect:=disk([-1/3,29/27], 0.03, color=blue): |
| > |
Cubic:=plot(f(x),x=-1..1,y=0..2,color=black,thickness=2,
title=`A cubic`): |
| > |
display(Cubic,Max,Min,Inflect); |
![[Plot]](images/plotting_12.gif)
Example 2: Drawing in asymptotes.
| > |
restart;with(plots):with(plottools): |
Warning, the name changecoords has been redefined
Warning, the assigned name arrow now has a global binding
| > |
f := x -> (2*x+1)/(x-1); |
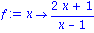

| > |
limit(f(x),x=infinity); |
| > |
limit(f(x),x=-infinity); |
Of course, it is very easy to find these asymptotes by hand, or in your head. The
line
command, used below, is in plottools and draws a line connected two points. The option "linestyle=3" produces a dashed line.
| > |
VA := line([1,-10], [1,10], color=red, linestyle=3): |
| > |
HA := line([-10,2], [10,2], color=red, linestyle=3): |
| > |
RatFunc:=plot(f(x),x=-10..10,y=-10..10,discont=true,
color=black,thickness=2): |
| > |
display(RatFunc,VA,HA); |
![[Plot]](images/plotting_15.gif)
Example 3: Another example.
| > |
restart;with(plots):with(plottools): |
Warning, the name changecoords has been redefined
Warning, the assigned name arrow now has a global binding
| > |
f := x -> (exp(x)+2*exp(-x))/(2*exp(x)+exp(-x)); |
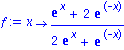
First we compute the limits. You should check these by hand.
| > |
limit(f(x),x=infinity); |
| > |
limit(f(x),x=-infinity); |
Next we look for critical numbers. First we look for places where f'(x) = 0.
| > |
Df:= x -> diff(f(x),x); |
When Malpe does not respond, there are no solutions. In order to see if there are places where f'(x) is undefined we need to see f'(x).
This is a bit messy.
It is clear that f'(x) is always defined. Next we look for inflection points. It is obvious that f''(x) is always defined. Why? Thus we just look for solutions to f''(x)=0. As it truns out there is only one inflection point and below I save it as Xinflect.
| > |
Xinflect:=solve(diff(f(x),x$2)=0); |


Thus, there are no extrema and only one inflection point.
| > |
Inflect:=disk([Xinflect,Yinflect], 0.1 ,color=blue): |
| > |
HA1:=line([-4,1/2],[4,1/2], color=red, linestyle=3): |
| > |
HA2:=line([-4,2],[4,2], color=red, linestyle=3): |
| > |
ExpFunc:=plot(f(x),x=-4..4,y=0..3,color=black,thickness=2): |
| > |
display(ExpFunc,HA1,HA2,Inflect); |
![[Plot]](images/plotting_19.gif)
Example 4: Dividing into sections.
| > |
restart;with(plots):with(plottools): |
Plot the function f(x)=(x^2-4)/(x^4+1) . Label the extrema and inflection points. You should do a quick sketch by hand. Notice the denominator is never zero. The function is zero at x = 2 and -2. Finally the limit as x goes to +infinity or -infinity is clearly zero.
| > |
f:= x -> (x^2-4)/(x^4+1); |
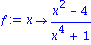
STEP 1: We do a first plot to get a feel for the function.
| > |
plot(f(x),x=-5..5,y=-5..5,color=black,thickness=2); |
![[Plot]](images/plotting_21.gif)
This looks different than our hand plot in class. We may need to plot it in sections. After some experimenting I came up with this. I plotted the function from [-10,-2] and restricted the y range. The plot over [2,10] will be the mirror image since the function is even.
| > |
plot(f(x),x=-10..-2,y=0..0.1,color=black,thickness=2); |
![[Plot]](images/plotting_22.gif)
STEP 2: Find the extrema.
| > |
simplify("); (The double quote says to insert the output of the command last executed.) |
So one zero of f'(x) is at x=0. For the others we solve . Let .
Then or . But the second is negative so won't be real. Thus, x is plus or minus .
Let's convert this to decimal form.
STEP 3: We compute f''(x).
| > |
simplify(diff(f(x),x$2)); |
The
solve
command is cannot handle this function in the mannor we want: it will give a messy formula for finding all complex roots. (Try it.) Instead we use
fsolve
, a floating-point solver.
| > |
fsolve(3*a^4-12*a^2+1-40*a^3+24*a,a,real); |
Two of these are negative. We only want the square roots of the positive ones.
| > |
sqrt(.6762337382); sqrt(13.58430522); |
Thus, we have four inflection points (plus and minus these two numbers).
STEP 4: We put it all together a make a nice plot (in sections).
| > |
Section1:=plot(f(x), x=-10..-2, y=0..0.1, color=black,thickness=2): |
| > |
Section2:=plot(f(x), x=-2..2, y=-5..0.1, color=black,thickness=2): |
| > |
Section3:=plot(f(x), x=2..10, y=0..0.1, color=black,thickness=2):
|
| > |
Max1:=ellipse([-sqrt(4+sqrt(17)),f(sqrt(4+sqrt(17)))],0.05,0.003,filled=true ,color=green): (I am using the
ellipse
command to overcome a scaling distortion problem.) |
| > |
Min:=disk([0,-4],0.05,color=green): |
| > |
Max2:=ellipse([sqrt(4+sqrt(17)),f(sqrt(4+sqrt(17)))], 0.05,0.003,filled=true ,color=green):
|
| > |
Inflect1:=ellipse([-3.685689246,f(-3.685689246)], 0.05, 0.003, filled=true ,color=blue): |
| > |
Inflect2:=disk([-.8223343226,f(-.8223343226)], 0.05 ,color=blue): |
| > |
Inflect3:=disk([0.8223343226,f(.8223343226) ], 0.05, color=blue): |
| > |
Inflect4:=ellipse([3.685689246, f(3.685689246)], 0.05, 0.003, filled=true, color=blue):
|
| > |
display(Section1,Max1,Inflect1); |
![[Plot]](images/plotting_23.gif)
| > |
display(Section2,Min,Inflect2,Inflect3); |
![[Plot]](images/plotting_24.gif)
| > |
display(Section3,Max2,Inflect4); |
![[Plot]](images/plotting_25.gif)
We are done. But notice that it looks as though the plots would not match up smoothly at -2 and +2. Explain why they do.
Problem 1: arcsin (ln(x))
In this problem you will analyze the graph of arcsin (ln(x)).
STEP 1: What is the domain? Justify your answer. You will likely need to review the arcsin and natural log functions.
STEP 2: Compute the first derivative. Is it ever zero? What happens to the tangent lines at the end points of the domain?
STEP 3: Compute the second derivative. Find any inflection points.
STEP 4: Plot the function. Mark any interesting points.
Problem 2: exp(-x/10)cos(x)
Graph the function y=exp(-x/10)cos(x), for x equals 0 to 10. Find a formula for the n-th relative maximum. Find a formula for the n-th relative minimum. Find the ratio between two relative maximums, and show that this ratio is always the same.
Problem 3: ln(f(x))
Let f(x)=x^2 + 4.
STEP 1: Graph y=f(x) & y=ln(f(x)) on the same graph.
STEP 2: Find and mark the extrema and inflection points of ln(f(x))
STEP 3: Repate steps 1 & 2 for f(x) = (x^2-1)^2 + 1/2.
STEP 3: Let f(x) be any positive differentiable function. Describe in words the graph of y=ln(f(x)). Where are its critical numbers compared to those of f(x)? Justify your answer.
Problem 4: arctan(f(x))
(a) Graph y=acrtan(x^2). Mark the extrema. What are the limits as x goes to +/- infinity?
(b) Graph y=acrtan((x-1)x(x+1)) Mark the extrema. What are the limits as x goes to +/- infinity?
(c) Compare the x locations of the extrema of y=arctan((x-1)x(x+1) with the x locations of the extrema of
y=(x-1)x(x+1).
Now let f(x) be any differentiable function.
(d) Show that the zeros of y=f(x) have the same x location as the zeros of y=arctan(f(x)).
(e) Show that the extrema of y=f(x) have the same x locatation as the extrema of y=arctan(f(x)).
(f) Graph y=arctan((sin(x)). Explain why what you see makes sense.
(f) What can you say about the limits of acrtan(f(x)) as x goes to +/- infinity?
(g) Graph by hand y=acrtan(f(x)) where f(x) is given by the graph below.
![[Plot]](images/plotting_26.gif)
![]()
![]()
![]()
![[Plot]](images/plotting_4.gif)
![]()
![[Plot]](images/plotting_6.gif)
![[Plot]](images/plotting_7.gif)
![[Plot]](images/plotting_8.gif)
![[Plot]](images/plotting_12.gif)
![[Plot]](images/plotting_15.gif)
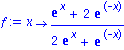
![[Plot]](images/plotting_19.gif)
![[Plot]](images/plotting_21.gif)
![[Plot]](images/plotting_22.gif)
![[Plot]](images/plotting_23.gif)
![[Plot]](images/plotting_24.gif)
![[Plot]](images/plotting_25.gif)
![[Plot]](images/plotting_26.gif)