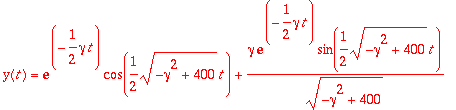
> with(DEtools):with(plots):

> m:=1:k:=100:

> dsolve({m*diff(y(t),t$2)+gamma*diff(y(t),t)+k*y(t)=0,y(0)=1,D(y)(0)=0},y(t));

>

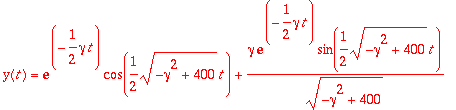
> anim:=animate(exp(-1/2*gamma*t)*cos(1/2*sqrt(-gamma^2+400)*t)+gamma*exp(-1/2*gamma*t)*sin(1/2*sqrt(-gamma^2+400)*t)/(sqrt(-gamma^2+400)),t=0..5,gamma=0..50,view=-2..2,frames=100,thickness=2,numpoints=100):

> g:=20:

> dsolve({m*diff(y(t),t$2)+g*diff(y(t),t)+k*y(t)=0,y(0)=1,D(y)(0)=0},y(t));

> critical:=plot(exp(-10*t)+10*exp(-10*t)*t,t=0..5,view=-2..2,color=black,thickness=2):

> display(anim,critical);

The black curve is the critical damping solution. In the animation damping increases from 0 to 50. Critical damping occurs at 20.