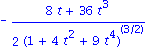
Finding the Osculating Plane (10.8 #38)

#38. Find the osculating plane to the curve r(t) = <t, t^2, t^3> when t=1.

Solution 1. It is easy to find r'(t) = <1, 2t, 3t^2> and then that |r'(t)| = sqrt(1+4t^2 + 9t^4). Thus

T(t) = <1, 2t, 3t^2>/sqrt(1+4t^2 + 9t^4).

At t=1 we get T(1) = <1/sqrt{14) , 2/sqrt(14), 3/sqrt(14) >

Now we have to find N(t) = T'(t)/|T'(t)|. But wait! For this aplicaition we really do not care that the length is 1. I will just find T'(t) and evaluate it at t=1.

>	diff(1/sqrt(1+4*t^2 + 9*t^4),t);

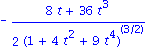
>	diff(2*t/sqrt(1+4*t^2 + 9*t^4) ,t);

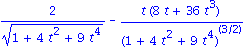
>	diff(3*t^2/sqrt(1+4*t^2 + 9*t^4),t);

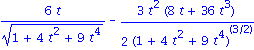
At t=1 we get T'(1) = <-22/(14*sqrt(14)), 2/sqrt(14) - 44/(14*sqrt(14), 6/sqrt(14) - 66/(14*sqrt(14)>.

But we just want any two vectors parallel to T(1) and N(1). Let V = sqrt(14)*T(1) = <1, 2, 3> and W = 14*sqrt(14)*T'(1) = <-22, -16, 18 >. Now V x W will be normal to the osculating plane.

>	with(LinearAlgebra):

>

>	CrossProduct(<1, 2, 3> ,<-22, -16, 18>);

Notice 84/28 = 3, so we can rescale and use <3, -3, 1> as our normal vector. So, the equation for the osculating plane is 3x-3y+z = D. We can find D since we know (1,1,1) is on the plane. The final answer is

                                3x-3y+z = 1.  

>	Solution 2.

Turns out there is a short cut!

>	with(VectorCalculus):

>	B := Binormal( t -> <t,t^2,t^3> ):

>

B(1);

The format is a little different. ex means the unit vector i, and so on. Since we don't care about the length of B we can just use <3, -3, 1> and proceed as in Solution 1.

>

restart;

Graph. Just for fun I will graph the curve and the osculating plane. The print out may not be that great.

>	with(plots):

Warning, the name changecoords has been redefined

>	sc:=spacecurve([t,t^2,t^3],t=0..2,color=black,thickness=3):

>	opl:=plot3d(1-3*x+3*y,x=0.5..1.5,y=0.5..1.5):

>	display3d(sc,opl);

>