The Mark McGwire Problem
By A. Sample
Introduction: This project is based on problem #18 in Section 2.7. We shall analyze the motion of a baseball with air resistance. The object is to hit a baseball over a 10 ft wall 350 ft away from the batter. We will show that the optimal initial angle for the ball's trajectory is, appoximately, 37 degrees, and that the minimine initial velocity for the ball is, approximately, 145 ft/sec.
Model:
Let
be the velocity in the
direction, and let
be velocity in the
direction. We shall use
for the acceleration due to gravity and
for the coefficient of air resistance. When doing numerical calculations we shall take
to be 32 ft/sec-sec and
to be 0.2 inverse seconds , as suggested by the textbook. The differential equations we shall use to model the motion of the baseball are
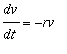and
.
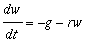Thus, we are assuming the force due to air resistance is proportional to the velocity, but in the opposite direction.
Step 1:
First we shall find
and
in terms of the initial speed
andthe initial angle of elevation
. We break down the initial velocity into its
and
component
s
:
and
. Then solving the differantial equations gives
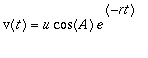and
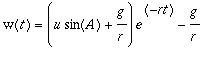
Step 2:
Now we must find the equations of motion, that is we must find x(t) and
as functions of time
. For initial conditions we shall use
and
. Later we shall take
to be 3 ft. high. This yields,
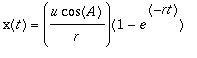and
.
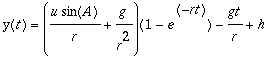Step 3:
To give the reader a better feel for the dynamics represented by these equaitions we shall plot the baseball trajectories for several different values of the initial angle
. Let
,
, and
We shall vary
from 0 to
in incriments of
.
> A:=Pi*i/12:
>
plot({seq([750*cos(A)*(1-exp(-t/5)),(750*sin(A) + 800)*(1-exp(-t/5))+3-160*t,t=0..10],
i=0..6)},0..500,0..250,color=black,thickness=2);
![[Maple Plot]](images/McGwire35.gif)
A visual inspection suggests that two of the hits made it over the fence.
Next we shall do a plot with a fixed angle of
but with varying the initial velocity form
50 to 200 ft/sec in incriments to 25.
> A:=Pi/6:
> u:=50+25*i:
>
plot({seq([5*u*cos(A)*(1-exp(-t/5)),(5*u*sin(A) + 800)*(1-exp(-t/5))+3-160*t,t=0..10],
i=0..6)},0..600,0..150,color=black,thickness=2);
![[Maple Plot]](images/McGwire37.gif)
Step 4:
Now comes the hard part. We want to find the optimal value of
so that
can be as small as possible, under the constrant that the ball takes it over the fence. That is, it is not enough simply to find the value of
that maximizes the distance the ball travels and then find the smallest value of
that gets the ball over the fence for that angle. It may be that a smaller
with a different initial angle would get the ball over the fence even though the ball might not travel as far.
We shall proceed as follows. First we solve for
as a function of
,
, and
. Then we set
. Thus incorporating the constrant that the ball just makes it over the fence. This will give a relation between
and
. To find the minimum
and hence the optimum
we need to find the derivative
and set it equal to zero. Unfortunately, we were unable to find isolate
or find
by implicit differentation, either by hand or with computer assistance. Thus, we resorted to plotting the relation
as a function of
vs
, and zoming in on its unique minimum.
Since
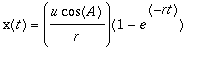we can solve for
and get
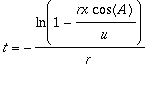. Substituting this into the equation for
gives us the following,
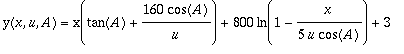. Since we require that
this last equation reduces to
.
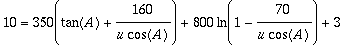The reader can perhaps appreciate the diffeculty in finding
. Below we plot this relation and estimate its minimum.
> restart;
Note: restart is needed to reset the value of
. After much "zooming in" the plot below shows the approximate minimum value of
.
>
plots[implicitplot](10 = 350*(tan(A) + 160/(u*cos(A))) +
800*ln(1 - 70/(u*cos(A))) + 3,
A=0.643..0.644,u=145.337..145.338,color=black,grid=[50,50]);
![[Maple Plot]](images/McGwire68.gif)
>
>
Conclusion:
Using the graph above we conclude that the opitmal value of the initail angle
is .6437 radians or 37 degress and that this corresponds to a minumum value of the initial velocity of the baseball of
ft/sec.