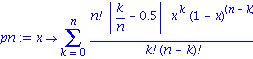
Bernstein Polynomial Approximations
EXAMPLE 1: Find the first value of n such that the nth Bernstein polynomial for f(x) = |x-0.5| has ||pn - f|| < 0.1.
| > | pn:= x-> sum((n!/k!/(n-k)!)*abs(k/n-0.5)*x^k*(1-x)^(n-k),k=0..n); |
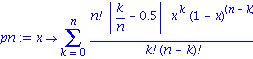
| > | n:=15; |
![]()
| > | plot([0.1,abs(x-0.5),pn(x)],x=0..1,color=[black,gray,black],
linestyle=[2,1,1],thickness=2); |
![[Plot]](Images/Bernstein_3.gif)
| > | pn(0.5); |
![]()
| > | n:=16; |
![]()
| > | pn(0.5); |
![]()
The answer is n=16.
EXAMPLE 2: Repeat for f(x) = | |x-0.5| - 0.25| and ||pn - f||<0.02.
| > | f:=x-> abs(abs(x-0.5)-0.25); |
![]()
| > | pn:= x-> sum((n!/k!/(n-k)!)*f(k/n)*x^k*(1-x)^(n-k),k=0..n); |
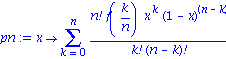
| > | n:=398; |
![]()
| > | plot([0.02,0.23,f(x),pn(x)],x=0..1,color=[black,black,gray,black],
linestyle=[2,2,1,1],thickness=2); |
![[Plot]](Images/Bernstein_10.gif)
| > | pn(0.5); |
![]()
The answer is n=398.