AnimationTriwave.mw
Vibrating String Examples with Animations
This is the example done in class. Below is the formula we found for c_n.
| > |
c:= n -> 8*sin(n*Pi/2)/(n^\2*Pi^2); |
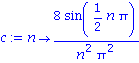
| > |
N:=100: # Number of terms to use. |
| > |
animate({sum((c(n)*sin(n*Pi*x/2)*cos(n*Pi*t/2)), n=1..N)}, x=0..2, t=0..4, frames=100, thickness=2); |
![[Plot]](Images/AnimationTriwave_2.gif)
Another example.The function is given below.
| > |
f := x -> piecewise(x<=1, x, (-1/2)*x+3/2); |
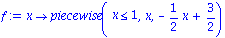
| > |
plot(f(x), x=0..3, thickness=2); |
![[Plot]](Images/AnimationTriwave_4.gif)
We will just leave the c_n as an integral.
| > |
c := n -> (2/3)*int(f(x)*sin(n*Pi*x/3) , x=0..3); |
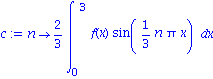
| > |
animate({sum((c(n)*sin(n*Pi*x/3)*cos(n*Pi*t/3)), n=1..N)}, x=0..3, t=0..6, frames=100, thickness=2); |
![[Plot]](Images/AnimationTriwave_6.gif)
Another Example.
| > |
f := x -> piecewise(x<1,0,x<2,x-1,x<3,-x+3,0); |
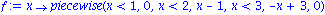
| > |
plot(f(x),x=0..4,thickness=2); |
![[Plot]](Images/AnimationTriwave_8.gif)
| > |
c := n -> (2/4)*int(f(x)*sin(n*Pi*x/4) , x=0..4); |
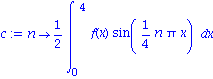
| > |
animate({sum((c(n)*sin(n*Pi*x/4)*cos(n*Pi*t/4)), n=1..N)}, x=0..4, t=0..8, frames=100, thickness=2); |
![[Plot]](Images/AnimationTriwave_10.gif)
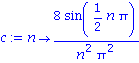
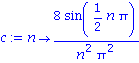
![[Plot]](Images/AnimationTriwave_2.gif)
![]()
![[Plot]](Images/AnimationTriwave_4.gif)
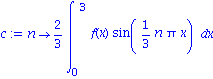
![[Plot]](Images/AnimationTriwave_6.gif)
![]()
![[Plot]](Images/AnimationTriwave_8.gif)
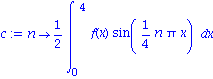
![[Plot]](Images/AnimationTriwave_10.gif)